Neighbourhood filters (introduction)
Prerequisites
Before starting this lesson, you should be familiar with:
Learning Objectives
After completing this lesson, learners should be able to:
Understand the basic principle of a neighbourhood filter.
Apply a mean filter to an image.
Motivation
Images are quite often noisy or have other issues that make them hard to segment, e.g. by means of a simple intensity threshold. Neighbourhood filters are a very important (maybe the most important) means to enhanced images in a sense of making them more amendable for segmentation.
Concept map
Example figure
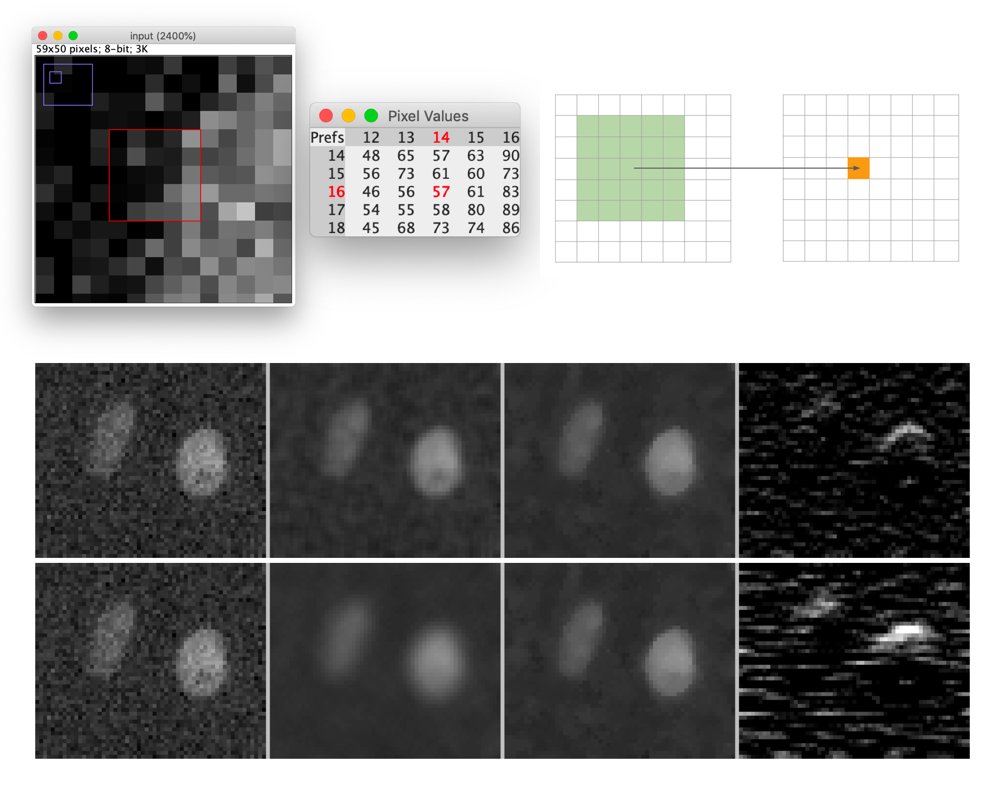
Neighbourhood filters
Neighborhood filters comprise two ingredients: a definition of the pixel neighbourhood (size and shape) and a mathematical recipe what to compute on this neighbourhood. The result of this computation will be used to replace the value of the central pixel in the neighbourhood. This procedure can be applied to several (all) pixels of an image to obtain a filtered image. The animation shows a square neighbourhoods (3x3) applied to the inner pixels of the image.
There are really tons of different neighborhood filters, and you can invent a new one!

The neighbourhoods
The neighborhood of a pixel is also called a structuring element and can have various sizes and shapes. Here, we use one of the simplest and most widely used neighbourhoods, namely a circular neighborhood, which is defined by a certain radius. We will explore other shapes of structuring elements in more detail in a dedicated module.
The math
There are really many many ways how to cleverly compute on a pixel neighborhood. For example, one class of computations is called convolutional filters, another is called rank filters. Here, we focus on the relatively simple mean filter, which is the mean filter.
Best practice
As usual, everything depends one the scientific question, but maybe one could say to use a filter that changes the image as little as possible.
Activity
- Open image xy_8bit__noisy_two_nuclei.tif
- Explore the effect of a mean filter of different sizes.
- Find the minimal size of a mean filter that enables binarization of the image into two forground objects (i.e. the nuclei).
ImageJ Macro & GUI
run("Close All"); // File › Open... open("https://github.com/NEUBIAS/training-resources/raw/master/image_data/xy_8bit__noisy_two_nuclei.tif"); // Image › Rename... rename("input"); // Image › Duplicate... run("Duplicate...", "title=mean_1" ); // Process › Filters › Mean... run("Mean...", "radius=1"); selectWindow("input"); run("Duplicate...", "title=mean_7" ); run("Mean...", "radius=7"); run("Tile");
Exercises
Show exercises for:ImageJ Macro & GUI
Exercise 1
- Open xy_8bit__nuclei_very_noisy.tif
- Apply a mean filter ([Process > Filters > Mean…]) to the image such that you can binarise the image into exactly three disjoint foreground regions (the three nuclei). It is helpful to first duplicate the image [Image > Duplicate …] or [Ctrl-Shift-D]
- What is the smallest size for the mean filter that does the job?
- What happens if the filter size increases?
Solution
run("Close All"); // File › Open... open("https://github.com/NEUBIAS/training-resources/raw/master/image_data/xy_8bit__nuclei_very_noisy.tif"); // Process › Filters › Mean... run("Mean...", "radius=2"); // Image › Adjust › Threshold... setThreshold(29, 255); setOption("BlackBackground", true); run("Convert to Mask");Exercise 2
Sometimes you would like to find out how the structuring-element (the neighbourhood) of a filter looks like. One way to do this is to apply a filter to a single white pixel and look at the resulting form.
- Open xy_8bit_binary__one_foreground_pixel.tif
- Apply a Maximum filter to the image [Process > Filters > Maxima…] the resulting image is the structuring element of your filter
Solution
run("Close All"); // File > Open... open("https://github.com/NEUBIAS/training-resources/raw/master/image_data/xy_8bit_binary__one_foreground_pixel.tif") // Duplicate the image Image > Duplicate... run("Duplicate...", "title=radius2"); // Maximum filter Process › Filters › Maximum... run("Maximum...", "radius=2");
Assessment
Fill in the blanks
Fill in the blanks, using these words: decrease, increase, size, structuring element, large
- A synonym for neighbourhood is __
- The filter radius characterize the filter ___
- ___ filter size can cause a loss of details in the filtered image
- Filter can be used to __ the noise in an image
- The usage of filters can __ the quality of image segmentation/binarization
Solution
- A synonym for neighbourhood is structuring element
- The filter radius characterize the filter size
- large filter size can cause a loss of details in the filtered image
- Filter can be used to decrease the noise in an image
- The usage of filters can increase the quality of image segmentation/binarization
Follow-up material
We recommend reading these modules next:
Learn more: