This lesson is still being designed and assembled (Pre-Alpha version)

Median filter

Prerequisites

Before starting this lesson, you should be familiar with:

Learning Objectives

After completing this lesson, learners should be able to:

  • Understand in detail what happens when applying a median filter to an image

Motivation

The median filter is a rank filter and is one of the most popular filters for reducing noise in microscopy images. While the median filter has indeed many good properties, it should be - like any other filter - used with care and a good understanding of its properties.

Concept map

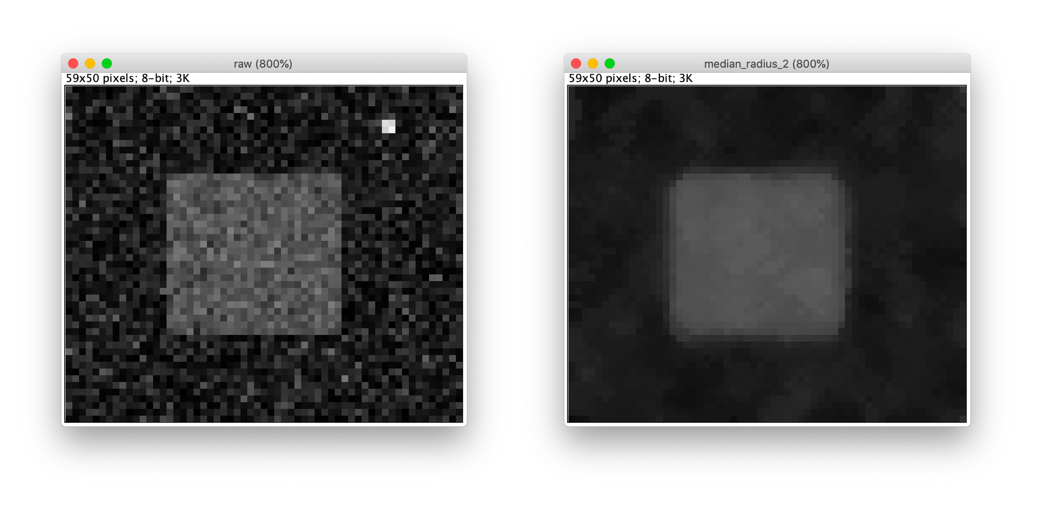
graph TD pixel --> NE("neighbourhood pixel values") NE --> median median --> MF("median filtered pixel value")

Example figure

Median filter example. Left - Raw; Right - After a 5x5 median filter.

Properties of median filter

The median filter is based on ranking the pixels in the neighbourhood

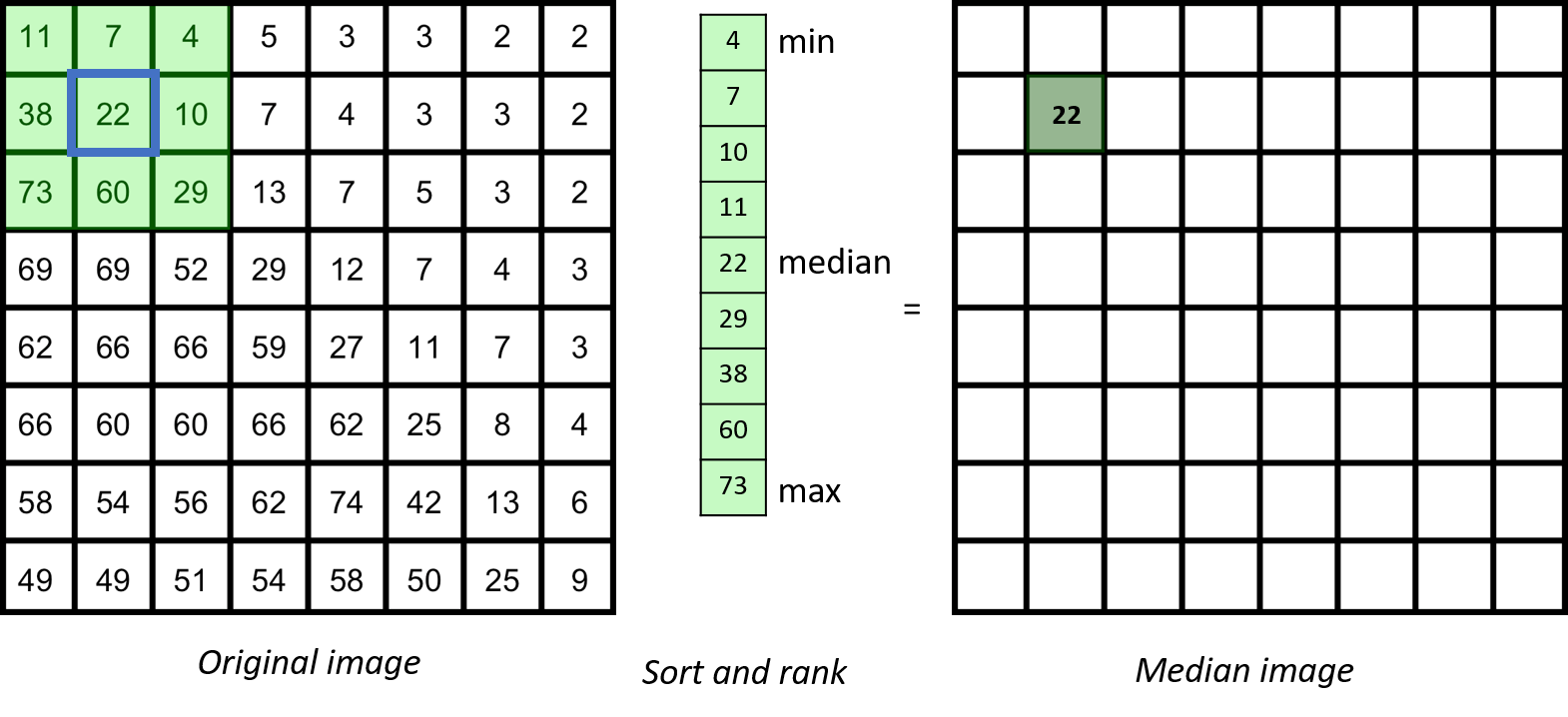
In general, for any neighbourhood filter, if the spatial extend of the neighbourhood is significantly (maybe three-fold) smaller than the smallest spatial length scale that you care about, you are on the safe side.

However, in biology, microscopy images are often containing relevant information down to the level of a single pixel. Thus, you typically have to deal with the fact that filtering may alter your image in a significant way. To judge whether this may affect your scientific conclusions you therefore should study the effect of filters in some detail.

Although a median filter typically is applied to a noisy gray-scale image, understanding its properties is easier when looking at a binary image.

From inspecting the effect of the median filter on above test image, one could say that a median filter

  • is edge preserving
  • cuts off at convex regions
  • fills in at concave regions
  • completely removes structures whose shortest axis is smaller than the filter width

Activity

Use example images that are relevant to your science and explore in detail what happens when applying a median filter. On purpose, increase the neighbourhood to an extend where your structures of interest become clearly compromised. Do some of all of these activities.

Show activity for:

ImageJ GUI & Macro median

run("Close All");

//File > Open...
open("https://github.com/NEUBIAS/training-resources/raw/master/image_data/xy_8bit__two_noisy_squares_different_size.tif");
// Image > Duplicate...
run("Duplicate...", "title=Median_1");
// Image > Duplicate...
run("Duplicate...", "title=Median_2");
// Image > Duplicate...
run("Duplicate...", "title=Median_5");

selectWindow("Median_1");
// Process › Filters › Median...
run("Median...", "radius=1");

selectWindow("Median_2");
// Process › Filters › Median...
run("Median...", "radius=2");

selectWindow("Median_5");
// Process › Filters › Median...
run("Median...", "radius=5");
run("Tile")

ImageJ GUI & Macro mean

run("Close All");

//File > Open...
open("https://github.com/NEUBIAS/training-resources/raw/master/image_data/xy_8bit__two_noisy_squares_different_size.tif");
// Image > Duplicate...
run("Duplicate...", "title=Mean_1");
// Image > Duplicate...
run("Duplicate...", "title=Mean_2");
// Image > Duplicate...
run("Duplicate...", "title=Mean_5");

selectWindow("Median_1");
// Process › Filters › Mean...
run("Mean...", "radius=1");

selectWindow("Mean_2");
// Process › Filters › Mean...
run("Mean...", "radius=2");

selectWindow("Mean_5");
// Process › Filters › Mean...
run("Mean...", "radius=5");
run("Tile")

Exercises

Show exercises for:

ImageJ GUI

Exercise 1

  • Open xy_16bit__microtubules.tif
  • Apply median filter with radius 1 and 3, respectively
  • Estimate the width of microtubules for non-filtered and filtered images using line profile, [Analyze > Plot Profile]
  • What happens if you median filter with radius above 10?
  • What happens to the microtubule width if you mean filter with radius 3

Solution

  • [File > Open …] xy_16bit__microtubules.tif
  • [Image > Duplicate] name small_median
  • [Image > Duplicate] name large_median
  • on small_median [Process > Filters > Median] radius 1
  • on large_median [Process > Filters > Median] radius 3
  • Draw a line with a line tool orthogonal to the MTs
  • Measure line width using [Analyze > Plot Profile] or [Ctrl-K]
  • Estimate width or in profile window [Data» > Add fit…] and [Fit function > Gaussian] the parameter d
    is a proxy for the width (d = sigma).
  • For radii larger than 10 the microtubules disappear
  • A mean filter with radius 3 will increase the apparent width (blur) the microtubules

Exercise 2

  • Open xy_8bit__nuclei_noisy_different_intensity.tif
  • Estimate radius of nuclei
  • Apply median filter smaller than nucleus radius
  • Apply median filter larger than nucleus radius
  • Which radius can be use to
    • suppress noise
    • remove dark spot in one of the nuclei
    • remove both nuclei
  • Compare median filter to mean filter of same radii
    • What are the advantages of a median filter?
    • What are the advantages of a mean filter?

Solution

  • [File > Open …] xy_8bit__nuclei_noisy_different_intensity.tif
  • Draw a line with a line along one of the nuclei and measure radius. About 7 px
  • Apply median filter smaller than nucleus radius. noise is suppressed
  • Apply median filter larger than nucleus radius: nuclei are shrinking
  • Which radius can be use to
    • suppress noise 2
    • remove dark spot in one of the nuclei 1
    • remove both nuclei 20
  • Compare median filter to mean filter of same radii
    • What are the advantages of a median filter? edge preserving
    • What are the advantages of a mean filter? small structure preserving

Assessment

True or false?

  1. Median filter is just another name for mean filter.
  2. Small structures can completely disappear from an image when applying a median filter.

Solution

  1. Median filter is just another name for mean filter. FALSE
  2. Small structures can completely disappear from an image when applying a median filter. TRUE

Follow-up material

We recommend reading these modules next:

Learn more: